Cómo funciona el interés compuesto: La fórmula del ahorro a largo plazo

Recuerdo la primera vez que leí sobre Warren Buffet en la biografía de Alice Schroeder, una autorizada estadounidense en temas financieros. Ahí no solo se explica cómo este gran inversor logró conseguir una rentabilidad extraordinaria, sino que también se aborda su filosofía financiera basada en la inversión temprana, la acumulación, y el uso estratégico del interés compuesto. Esta poderosa herramienta financiera actúa como un multiplicador silencioso que transforma cantidades menores y constantes aportaciones en un crecimiento sorprendente del capital con el tiempo.

Es como subir una montaña: puede parecer un esfuerzo menor, pero con periodicidad y paciencia, uno logra una renta estable y creciente. A diferencia del interés simple, que solo se calcula sobre la partida inicial, el compuesto reinvierte los rendimientos generados, haciendo que el dinero crezca de forma exponencial a medida que pasa el tiempo.

El Instituto BBVA lo ha ilustrado con la metáfora de una montaña que se eleva a medida que transcurre el sendero. Si un individuo decide invertir de forma constante, aunque sea una cantidad menor, aplicando una buena tasa de interés y con suficiente horizonte, la rentabilidad puede ser mucho mayor. Esta es una de las filosofías que sigo como empresario: saber cuándo y cómo aplicar operaciones financieras para obtener el máximo rendimiento sin necesidad de asumir grandes créditos o riesgos.

En este título, más que solo números, trata de comprender los elementos fundamentales que permiten que el ahorro sea efectivo. Así se puede rebajar la ansiedad financiera y aprovechar al máximo el potencial del dinero. Como dice el propio Buffet, el conocimiento y el esfuerzo bien dirigidos superan cualquier ventaja de partida en la economía real.

¿Cómo funciona el interés compuesto?

Cuando mis padres me abrieron una cuenta de ahorro siendo niño, nunca imaginé el poder que tendría esa decisión años después. Al principio, los euros parecían estáticos, pero con el paso del tiempo y gracias a la aplicación del interés compuesto, ese pequeño depósito inicial comenzó a multiplicarse casi sin darme cuenta. A diferencia del interés simple, que solo aplica sobre el capital inicial, el compuesto va sumando los rendimientos obtenidos cada año, y esos beneficios también reportarán nuevas ganancias en el siguiente periodo.

Esta herramienta transforma una técnica aritmética en una palanca de crecimiento exponencial, donde el capital se mantiene cambiando y creciendo de manera progresiva. En un ejemplo real, si haces una inversión de 1.000 euros al 6% anual, el primer año tendrás 1.060, y al segundo ya estarás generando intereses sobre 1.060, no sobre 1.000. Así se crean oportunidades de ganancia sin necesidad de hacer un ingreso extra.

Hoy en día, cuando pienso en el futuro de mis hijos, sé que enseñarles sobre este tipo de capitalización es más valioso que cualquier juguete costoso. En el mercado actual, donde el tipo de interés nominal (TIN) puede variar, conocer cómo se aplican los efectos del interés compuesto marca la diferencia entre quienes solo ganan lo inicial y quienes logran una mayor rentabilidad.

Esta inversión se aplica recurrentemente, constantemente ingresan nuevos intereses que aumentan el total. Todo esto depende también de la tasa anual, del porcentaje que se elija, y de cuánto tiempo se mantenga la inversión. La base es clara: cuanto más largo el periodo, más crece la ganancia. Incluso iniciales cantidades pueden dar lugar a grandes beneficios si se deja que la matemática haga su magia.

En qué se diferencia del interés simple

Cuando abrí mi primera cuenta de ahorro, pensé que los intereses siempre se calculan igual, pero pronto descubrí que hay un mundo de diferencia entre el interés compuesto y el interés simple. El simple se calcula siempre sobre el mismo capital depositado, sin importar cuánto tiempo pase ni cuántos periodos transcurran. Por ejemplo, si al inicio inviertes 1.000 €, y la tasa es del 5%, obtendrás 50 € cada año, sin sumar esos beneficios al capital para el próximo cálculo. Así, el poder de crecer se queda estancado, como si el dinero solo se moviera en línea recta.

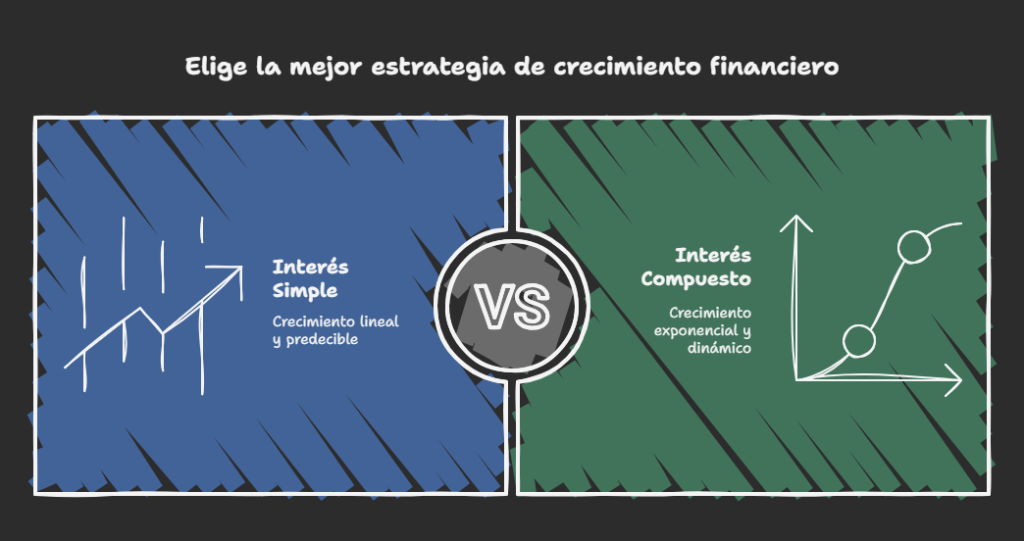
En cambio, el compuesto genera nuevos intereses en cada periodo, no solo por el capital original, sino también por las ganancias ya obtenidas. Cada suma se reinvierte, y es ahí donde nace su poder real: transforma una cantidad inicial en una curva ascendente de rendimiento. La diferencia no es solo matemática, es estratégica. Uno se limita a repetir; el otro multiplica. Y esa es la clave que, como inversor, cambió completamente mi manera de ver el dinero.

¿Cómo calcular el interés compuesto?

Recuerdo cuando empecé a invertir una pequeña cantidad: 110 euros. Quería entender cómo calcular el interés compuesto, pero la teoría me parecía algo enrevesada. Fue hasta que lo llevé a la práctica que todo tuvo más sentido. Imagina que depositas un capital inicial de 100 euros, con un interés anual del 10%. Al final del primer año, se generarán 10 euros de ingreso, por lo que el resultado final será 110 euros. Pero lo interesante ocurre sucesivamente: al aplicar ese mismo tipo de interés al segundo año, no se calcula solo sobre el monto original, sino también sobre los intereses generados.

Veamos qué pasaría: si llevas a cabo la operación, el resultado será 121 euros. ¿Por qué? Porque al final del segundo año, los 10 euros de interés del primer período también tienen su propio rendimiento. La fórmula exacta puede parecer técnica, pero en forma sencilla, consiste en multiplicar el capital por (1 + tasa de interés) elevado al número de años. Así, los intereses se ingresarán automáticamente en la cuenta y serán parte de los futuros cálculos. En mi experiencia, es preferible empezar cuanto antes: cuanto antes se mueva el dinero, mayores serán los beneficios a largo plazo. Nada como un buen ejemplo real para entender cómo un pequeño ingreso hoy se convierte en una base sólida mañana.

La fórmula del interés compuesto

Cuando descubrí el poder del interés compuesto, fue como ver cómo una simple inversión comenzaba a crecer por sí sola, casi como magia financiera. Todo parte de una fórmula que, aunque parece complicada al principio, se vuelve clara al entender su lógica. Si tienes un capital inicial (C0) de 100 euros y una tasa anual del 0,10 (es decir, 10%), el resultado final tras un año será de 110 euros. Pero lo fascinante ocurre después: al aplicar esa misma tasa al segundo año, no se parte del mismo monto, sino que se aplicaría sobre los intereses obtenidos anteriormente, aumentando así el total.

La fórmula completa para calcular el interés compuesto es: C0 x (1 + Ti)^t, donde “Ti” es la tasa de interés, y “t” es el tiempo o duración de la inversión. Al elevar la expresión a la potencia “^t”, estás sumando cada rendimiento al capital de manera acumulativa. Por ejemplo, si dejas tu dinero invertido por dos años, y mantienes las mismas condiciones, el monto final no será solo 110, sino 121 euros, ya que el interés generado en el primer año también trabaja por ti en el siguiente. Esta forma de utilizar el dinero es clave para quienes piensan a largo plazo, ya que, variando solo uno de estos factores, los beneficios pueden multiplicarse de manera exponencial.

La magia del interés compuesto

Cuando descubrí que con solo aportaciones mensuales de 100 euros podía llegar a tener más de 65.000 euros al final de mi vida laboral, entendí que el interés compuesto no es una fórmula, sino una de las herramientas más poderosas para potenciar nuestro dinero. Supón que haces pequeñas contribuciones cada mes, durante 25 años, con una tasa anual del 3%: el impacto de ese hábito es sorprendente. Si sumamos todo lo que has aportado, serían unos 30.000 euros, pero el monto acumulado alcanzará cifras que superen los 65.000 euros, gracias al efecto multiplicador de los intereses que se generan durante cada ciclo. Es el poder de hacer que tu capital inicial trabaje por ti, y que incluso el rendimiento anterior también crezca por su cuenta.

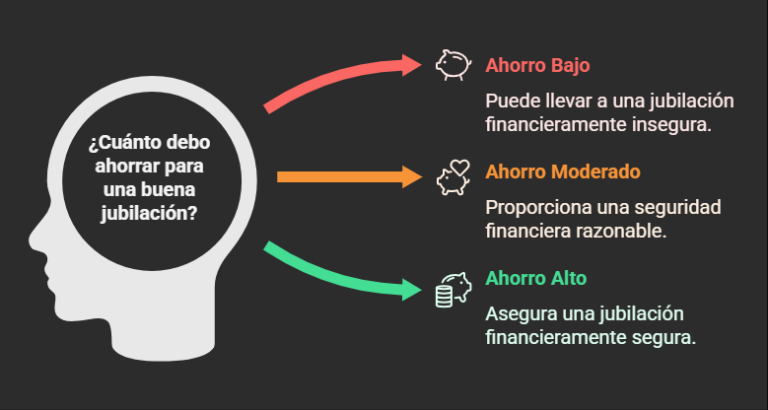
El objetivo de ahorrar no es solo ahorrar, sino proteger el valor de tu inversión frente a la inflación y dejar que con el tiempo gane fuerza. Por ejemplo, si empezaras con 10.000 euros y no hicieras más contribuciones, pero los dejaras 20 años con una tasa del 4% anual, el saldo final crecerá a 21.920 euros. Pero si en lugar de eso haces aportaciones importantes de 12 euros mensuales, tu ahorro podría llegar a los 14.260, y si las aumentas a 24, el total podría ser 20.192. Bajo el supuesto de que no haya retiros y que el interés se mantenga estable, es ideal buscar una estrategia de ahorrar constante y consciente. Que tu dinero no pierda valor: hazlo crecer con inteligencia.

Interés compuesto en un préstamo

Cuando pedí mi primer préstamo personal, no imaginaba cuánto afecta el interés compuesto al coste total. En el sistema francés de amortización, el más común, los intereses se calculan sobre el capital pendiente y se suman a cada cuota mensual, lo que hace que en los primeros períodos pagues más intereses que principal. Por ejemplo, si solicitas 1000 euros al 3% anual durante dos años, podrías pagar hasta 1.060,9 euros en total, y en el primer año, pagarían 60,9 euros solo en intereses.

En el segundo año, aunque las cuotas se mantengan, el tipo de interés compuesto hace que el saldo disminuya más lento. Este caso ilustra cómo el interés no solo se calcula al inicio, sino que se utiliza en cada periodo, y si no se entiende bien, uno termina por devolver mucho más de lo que pidió. Incluso pequeñas diferencias como 30,9 vs 42,98 euros por mes durante 30 años pueden representar una diferencia de 1.031,55 frente a 1030 euros que no se nota al principio, pero pesa al final.